SeFa — Finding Semantic Vectors in Latent Space for GANs

Paper Explained: SeFa — Closed-Form Factorization of Latent Semantics in GANs

Originally posted on My Medium.

Motivation

The generator in GANs usually takes a randomly sampled latent vector z as the input and generates a high-fidelity image. By changing the latent vector z, we can change the output image.

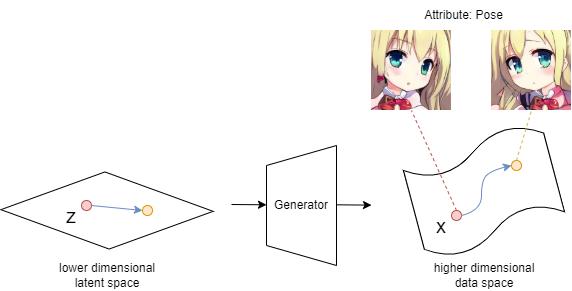
However, in order to change a specific attribute in the output image (e.g. hair color, facial expression, pose, gender, etc.), we need to know the specific direction in which to move our latent vector z.

Some previous works have tried to interpret the latent semantics in a supervised fashion. They usually label the dataset and train an attribute classifier to predict the labels of the images, and then calculate the direction vectors of the latent code z for each label. Even though there were some unsupervised methods for this task, most of them require model training and data sampling.

Nonetheless, this paper proposed a closed-form and unsupervised method, named SeFa, to let us find out these direction vectors for altering different attributes in the output image without data sampling and model training.

A closed-form solution is a mathematical expression with a finite number of standard operations.

The word “unsupervised” means that we don’t need to label the dataset.

Moving Latent Code

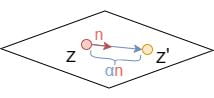
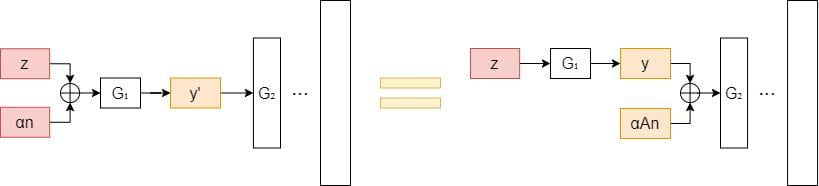
To change the latent code meaningfully, we need to first identify a semantically meaningful direction vector \textbf{n}. The new latent code is calculated as \textbf{z}'=\textbf{z}+\alpha\textbf{n}, where \alpha is the number of steps towards the direction \textbf{n}.

\text{edit}(G(\textbf{z}))=G(\textbf{z}')=G(\textbf{z}+\alpha\textbf{n})

where edit(…) denotes the editing operation

The problem is how do we find out the semantically meaningful direction vector \textbf{n}?

Related Work — PCA Approach

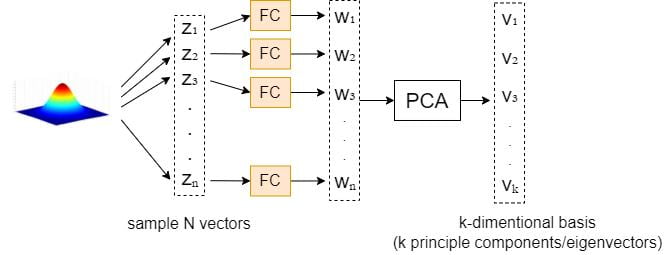
In a previously published paper GANSpace: Discovering Interpretable GAN Controls, Härkönen et al. performed Principal Component Analysis (PCA) on the sampled data to find out the primary direction vectors in the latent space.

Recall that PCA is a tool to find out axes of large variations

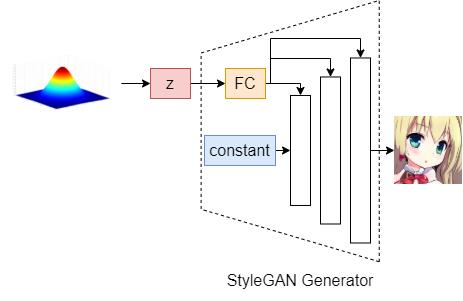
Let’s take the generator in StyleGAN as an example. The latent code \textbf{z} will be fed into a Fully-Connected layer (FC) before going into each intermediate layer.

The proposed method is as follows: we first sample N random vectors \{z_1, z_2, \dots, z_n\} and then feed them into the FC layer to get the projected outputs \{w_1, w_2, \dots, w_n\}. Hence, we apply PCA to these \{w_1, w_2, \dots, w_n\} values to get the k-dimensional basis \textbf{V}.

Given a new image defined by \textbf{w}, we can edit it by varying PCA coordinates \textbf{x} before feeding it to the synthesis network as follows.

\textbf{w}'=\textbf{w}+\textbf{Vx}

where each entry x_i of \textbf{x} is a separate control parameter. The entries x_i are initially zero.

Although this PCA method is unsupervised, it requires data sampling, which is inefficient. I mention this approach in this article because it bears a resemblance to today’s topic — SeFa.

SeFa — Semantic Factorization

State-of-the-art GAN models typically consist of multiple layers. Each layer learns a transformation from one space to another. This paper focuses on examining the first transformation, which can be formulated as an affine transformation as follows.

G_1(\textbf{z}) \triangleq \textbf{y} = \textbf{Az} + \textbf{b}

where \textbf{A} and \textbf{b} denote the weight and bias in the first transformation respectively

If we apply \textbf{z}'=\textbf{z}+\alpha\textbf{n} to the input latent code, the first transformation formula can be simplified as follows.

\begin{aligned}
\textbf{y}' \triangleq G_1(\textbf{z}') 
&= G_1(\textbf{z}+\alpha\textbf{n}) \\
&=\textbf{Az} + \textbf{b} + \alpha\textbf{An} \\
&= \textbf{y} + \alpha\textbf{An}
\end{aligned}

recall that G_1(\textbf{z})=\textbf{y}

Since G_1(\textbf{z}+\alpha\textbf{n}) = G_1(\textbf{z})+\alpha\textbf{An}, we know that if a latent code \textbf{z} and the direction vector \textbf{n} are given, the editing process can be achieved by adding \alpha\textbf{An} to the projected code after the transformation.

From this perspective, the weight parameter \textbf{A} should contain the essential knowledge of the image variation. Thus we aim to discover important latent directions by decomposing \textbf{A}.

The SeFa algorithm is similar to the previous PCA approach. But instead of applying PCA to the projected latent code G_1(\textbf{z})=\textbf{y}, it applies a very similar process to the weights of the projection layer (weights of G_1) directly.

Just like PCA, this process also aims to find out the direction vectors that can cause large variations after the projection of \textbf{A}. It is formulated as the following optimization problem.

\textbf{n}^* = \argmax_{ \{ \textbf{n} \in \mathbb{R}^d:\ \textbf{n}^T \textbf{n} = 1 \} } \left\| \textbf{An} \right\|_2^2

where \left\| \dots \right\|_2 denotes the L2-norm and \textbf{n} is a unit vector

To find out k most important directions \{n_1, n_2, \dots, n_k\}:

\textbf{N}^* = \argmax_{ \{ \textbf{N} \in \mathbb{R}^{d \times k}:\ \textbf{n}_i^T \textbf{n}_i = 1\ \forall i=1, \cdots, k \} } \sum_{i=1}^{k} \left\| \textbf{An}_i \right\|_2^2

where \textbf{N}=[ n_1, n_2, \dots, n_k ] correspond to the top-k semantics

To prevent the equation from producing a trivial solution when \left\| \textbf{n}_i \right\| \to \infty, we restrict \textbf{n}_i to be a unit vector and introduce the Lagrange multipliers \{\lambda_1, \lambda_2, \dots, \lambda_k\} into the equation.

\begin{aligned}
\textbf{N}^*
&= \argmax_{\textbf{N}\in\mathbb{R}^{d \times k}} \sum_{i=1}^{k} \left\| \textbf{An}_i \right\|_2^2 - \sum_{i=1}^{k} \lambda_i(\textbf{n}_i^T \textbf{n}_i - 1) \\
&= \argmax_{\textbf{N}\in\mathbb{R}^{d \times k}} \sum_{i=1}^{k}(\textbf{n}_i^T \textbf{A}^T \textbf{An}_i - \lambda_i \textbf{n}_i^T \textbf{n}_i + \lambda_i)
\end{aligned}

By taking the partial derivative on each \textbf{n}_i, we have:

\begin{aligned}
2\textbf{A}^T\textbf{An}_i - 2\lambda_i\textbf{n}_i &= 0 \\
\textbf{A}^T\textbf{An}_i &= \lambda_i\textbf{n}_i
\end{aligned}

As you can tell, this is very similar to PCA. The only difference is that the SeFa method replaced the covariance matrix S with \textbf{A}^T\textbf{A}, where \textbf{A} is the weight of G_1.

Instead of computing the eigenvectors of the covariance matrix, SeFa computes the eigenvectors of \textbf{A}^T\textbf{A}. By virtue of this, we don’t need to sample any data for computing the covariance matrix of the projected vectors. This makes the algorithm much easier and faster, and also makes it closed-form.

Generalizability

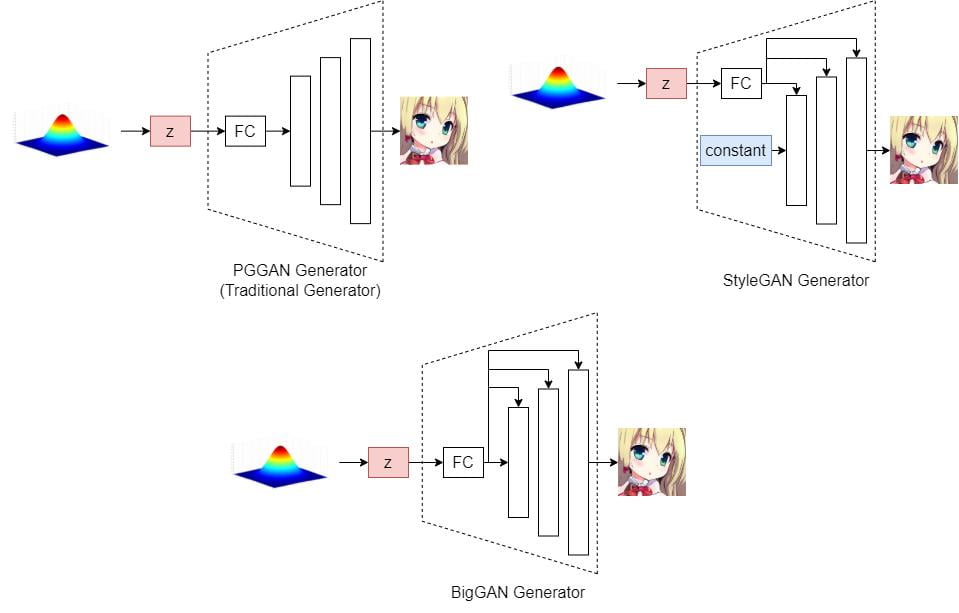
This paper has shown how they apply the SeFa algorithm to the following 3 types of GAN models: PGGAN, StyleGAN, and BigGANs. The following are brief diagrams showing how each of them feeds the latent vector \textbf{z} into their generators.

PGGAN

The PGGAN generator is just like the traditional generator, in which the latent code \textbf{z} is fed into a Fully-Connected layer (FC) before going into the synthesis network.

For this kind of generator structure, SeFa studies the transformation from
the latent code to the feature map. (aka. the weights of the first FC layer)

StyleGAN

In the StyleGAN generator, the latent code is transformed into a style code and then fed into each convolution layer.

The SeFa algorithm is flexible such that it supports interpreting all or any subset of layers. For this purpose, we concatenate the weight parameters (i.e. \textbf{A}) from all target layers along the first axis, forming a larger transformation matrix.

BigGAN

In the BigGAN generator, the latent code will be fed into both the initial feature map and each convolutional layer.

Hence, the analysis of BigGAN can be viewed as a combination of the above two types of GANs.

Results

References

[1] E. Härkönen, A. Hertzmann, J. Lehtinen and S. Paris, “GANSpace: Discovering Interpretable GAN Controls”, arXiv.org, 2022. https://arxiv.org/abs/2004.02546

[2] Y. Shen and B. Zhou, “Closed-Form Factorization of Latent Semantics in GANs”, arXiv.org, 2022. https://arxiv.org/abs/2007.06600