Originally posted on My Medium.

In Style Transfer and some generative networks, special normalization layers such as CIN, and AdaIN are used to control the style of the output image. But how and why does a normalization layer affect image style?

It is crucial to understand the rationale behind them in order to know why they are integrated into many modern neural network models.

Gram Matrix

The story starts with the first Neural Style Transfer paper — A Neural Algorithm of Artistic Style by Leon Gatys et al. published in 2015.

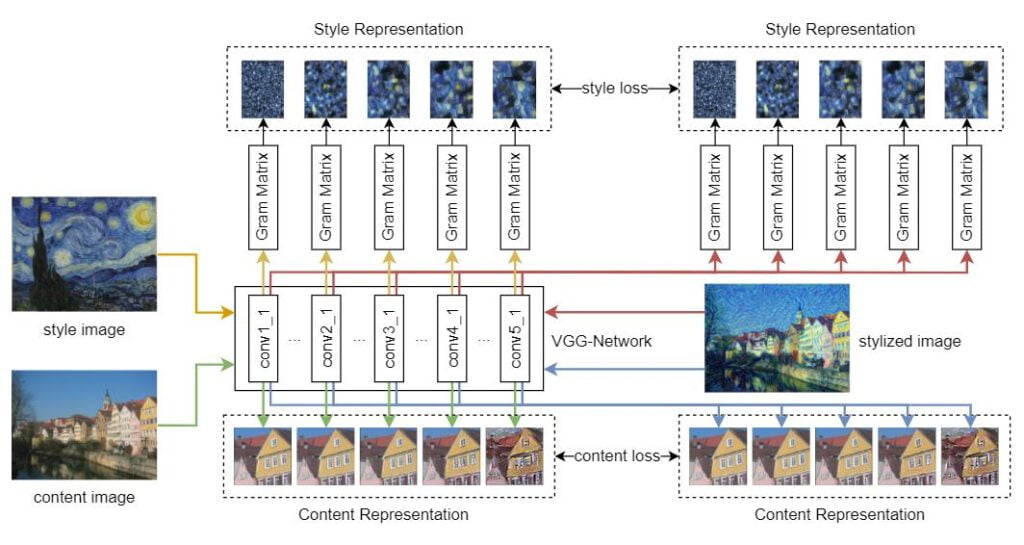
In Neural Style Transfer, the style loss is calculated as the distance between the Gram matrices of some CNN layer outputs of the target style image and your generated stylized image.

It is found that by using the Gram matrix, which computes the correlations between different filter responses from a CNN, we can extract the style representation of an image.

The following diagram shows how the Gram matrix is computed for one of the CNN layer outputs: conv1_1.

However, the paper did not explain why the Gram matrix is so effective in representing the style features.

Normalization Statistics

This mysterious property of the Gram matrix was then explained in Demystifying Neural Style Transfer paper published by Y, Li et al. in 2017.

The style of an image can be intrinsically represented by feature distributions in different layers / activations of a CNN.

The matching of the Gram matrices of activations of a CNN is equivalent to minimizing the maximum mean discrepancy (MMD) of the activation distributions.

In other words, the matching of Gram matrices (the style loss) tries to minimize the difference between the generated image and the style image’s activation distributions, which are the intrinsic representation of the style information of the two images.

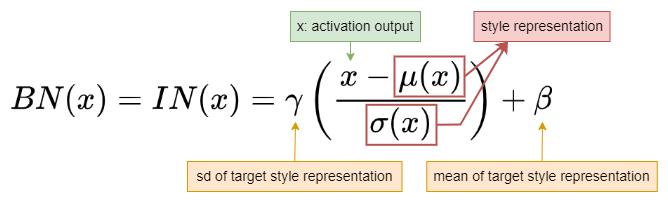
Further, the authors found that the statistics (i.e. mean and variance) of Batch Normalization (BN) layers contain the traits of different domains. The BN statistics of a certain layer can also represent the style.

Recall that the mean and variance of a normalization layer are calculated using the previous layer outputs. Therefore, if the previous layer is an activation layer, the mean and variance of the activations can be used to represent the style.

Now, instead of minimizing the Gram matrices of activations, we can actually minimize the mean and variance of activations between the generated image and the style image to do the style transfer. In improved style transfer networks, the Gram matrix is replaced by the L2 norm of the activation statistics of mean and variance.

However, style transfer is not the focus of today’s topic. All we need to know here is that the statistics of the normalization layer can be used to represent the style of an image.

Normalization Layer

In generative networks (e.g. GANs), how can we control the style of the generated image using normalization layers?

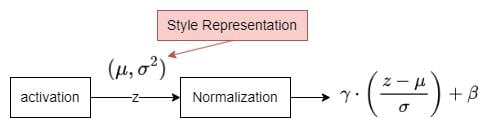
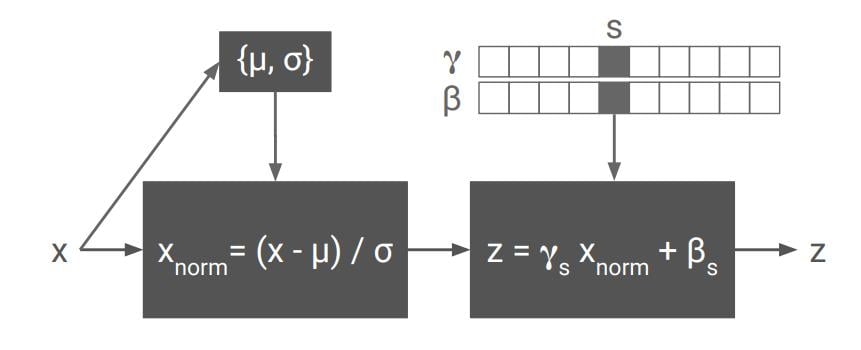
The intuition is that the normalization layer will map the activation distribution (μ, σ²) to another distribution (β, γ²). If we look at the Batch Normalization (BN) and Instance Normalization (IN) equations, we can observe this mapping easily.

1. Normalize the activation outputs by (x-μ)/σ
2. Scale it by multiplying γ and then shift it by adding β

Therefore, by controlling γ and β in the normalization layer, we can control the style of the output.

However, there is only one set of γ and β in each normalization layer. This makes it only able to learn one single style. To make the network learn multiple styles, we need some modified normalization layers. This is where CIN and AdaIN come into play.

CIN

Conditional Instance Normalization (CIN) is a simple way to learn multiple styles in the normalization layer. Here, γ and β are trainable vectors storing N styles. The CIN layer accepts two inputs:

1. The activation from the previous layer
2. The style label S (the id/index of the target style)

The input activation x is normalized across both spatial dimensions and subsequently scaled and shifted using style-dependent parameter vectors γs, βs where s indexes the style label

The flaw of CIN is that it can only learn N styles.

AdaIN
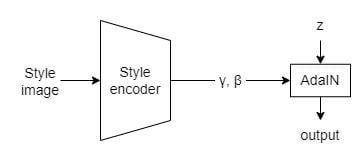
Adaptive Instance Normalization (AdaIN) is designed to solve this problem so it can learn any number of styles. It also accepts two inputs:

1. x: the activation from the previous layer
2. y: the style features (e.g. extracted from CNN) of your target style image

\text{AdaIN}(x,y)=\sigma(y)\left(\frac{x-\mu(x)}{\sigma(x)}\right)+\mu(y)

(μ(x), σ(x)) and (μ(y), σ(y)) are the statistics of x and y respectively

Note that there are no trainable variables in this AdaIN layer. All the means and variances can be directly calculated.

\text{AdaIN}(z,\gamma,\beta)=\gamma\left(\frac{z-\mu(z)}{\sigma(z)}\right)+\beta

z is the activation from the previous layer

Some models can even have a separate encoder learning to encode style into embedding spaces of γ and β, and then directly feed them into AdaIN as inputs.

Conclusion

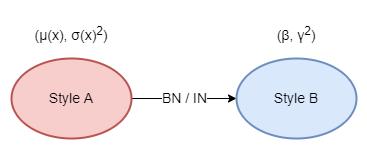
1. Activation distribution can represent the image style.
2. By mapping the mean and variance of the activations, we can translate the features from Style A to Style B.
3. The mapping of statistics can be done in a normalization layer.

References

• Gatys, L., Ecker, A. and Bethge, M., 2021. A Neural Algorithm of Artistic Style. Available at: https://arxiv.org/abs/1508.06576
• Li, Y., Wang, N., Liu, J., and Hou, X., 2021. Demystifying Neural Style Transfer. Available at: https://arxiv.org/abs/1701.01036
• Dumoulin, V., Shlens, J. and Kudlur, M., 2021. A Learned Representation For Artistic Style. Available at: https://arxiv.org/abs/1610.07629v5